Segregated by Design? Street Network Topological Structure and the Measurement of Urban Segregation

Abstract

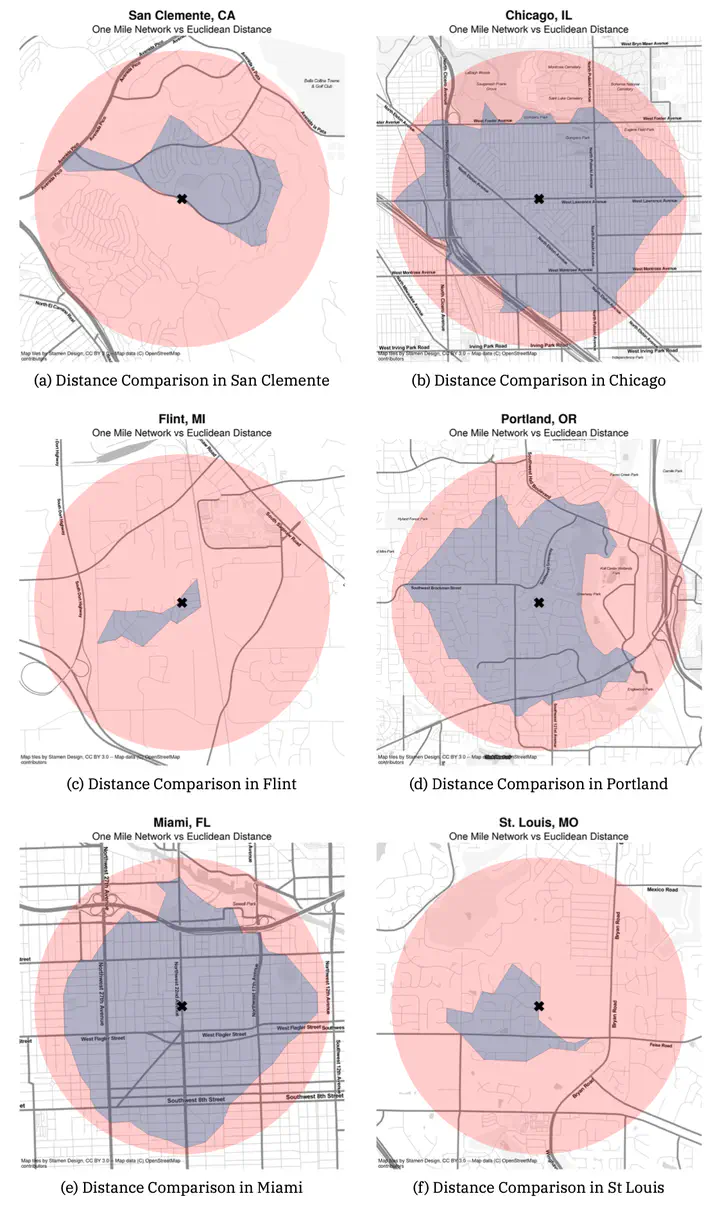
Racial residential segregation is a longstanding topic of focus across the disciplines of urban social science. Classically, segregation indices are calculated based on areal groupings (e.g., counties or census tracts), with more recent research exploring ways that spatial relationships can enter the equation. Spatial segregation measures embody the notion that proximity to one’s neighbors is a better specification of residential segregation than simply who resides together inside the same arbitrarily drawn polygon. Thus, they expand the notion of ``who is nearby’’ to include those who are geographically close to each polygon rather than a binary inside/outside distinction. Yet spatial segregation indices often resort to crude measurements of proximity, such as the Euclidean distance between observations, given the complexity and data requirements of calculating more theoretically appropriate measures, such as distance along the pedestrian travel network. In this paper, we examine the ramifications of such decisions. For each metropolitan region in the U.S., we compute both Euclidean and network-based spatial segregation indices. We use a novel inferential framework to examine the statistical significance of the difference between the two measures and following, we use features of the network topology (e.g., connectivity, circuity, throughput) to explain this difference using a series of regression models. We show that there is often a large difference between segregation indices when measured by these two strategies (which is frequently significant). Further, we explain which topology measures reduce the observed gap and discuss implications for urban planning and design paradigms.